Що таке ECDSA в біткоїні?

ECDSA (абревіатура від Elliptic Curves Digital Signature Algorithm , алгоритм побудови цифрового підпису з використанням еліптичних кривих) — це схема криптографії на основі еліптичних кривих (Elliptic Curve Cryptography або ECC).

Алгоритм ECDSA використовує еліптичну криву і кінцеве поле для створення підпису даних таким чином, що треті сторони можуть верифікувати автентичність підпису, а сторона, яка підписала, зберігає ексклюзивну можливість створювати підпис. У випадку біткоїна підписувані дані — це транзакція передачі права власності.

Хто і коли розробив концепцію ECC?

Концепцію криптографії на основі еліптичних кривих незалежно один від одного запропонували математики Ніл Кобліц і Віктор С. Міллер 1985 року. Хоча їхня модель стала проривом у криптографії, ECC не використовувалася широко до початку 2000-х, коли її впровадили інтернет-провайдери.

Як ECC застосовується в криптовалютах?

Криптографія, що лежить в основі схем цифрових підписів криптовалют, дає змогу здійснювати верифікацію транзакцій між двома сторонами в децентралізованій мережі.

ECC має значну перевагу над шифруванням за методом RSA. Розмір ключа, використовуваного для ECC, набагато менший за розмір ключа, необхідного для RSA. При цьому ECC забезпечує той самий рівень безпеки. Хоча шифрування за методом RSA в наші дні набагато ширше використовується в інтернеті, ECC — це більш ефективна форма RSA, що і служить причиною використання цієї криптографії в криптовалютах.

Хто і коли розробив ECDSA?

Концепцію ECDSA представив 1992 року канадський математик і криптограф Скотт Ванстоун.

Яке завдання виконує ECDSA?

Технологія в основі біткоїна переосмислює концепцію права власності. У традиційному сенсі володіти чим-небудь — будинком, грошовою сумою тощо. — означає або зберігати (фізично/юридично) цей об’єкт особисто, або передати на відповідальне зберігання довіреній структурі (наприклад, банку).

У разі біткоїна все інакше. Самі біткоїни не зберігаються ні центрально, ні локально, жодна структура не виступає в ролі їхнього кастодіана.

Біткоїни існують як записи в блокчейні, копії якого розподіляються мережею пов’язаних комп’ютерів. "Володіти" біткоїном означає мати можливість передавати контроль над ним іншому користувачеві, створюючи запис передачі в блокчейні. Що дає таку можливість? Доступ до пари ключів ECDSA — відкритого і закритого.

ECDSA має окремі процедури для підпису та для верифікації. Кожна процедура — це алгоритм, що складається з кількох арифметичних операцій. Алгоритм підпису використовує закритий ключ, алгоритм верифікації — відкритий ключ.

Що таке еліптична крива?

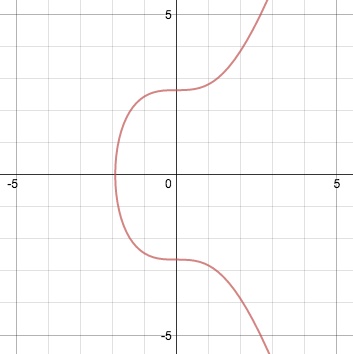
Алгебраїчно еліптична крива представлена як рівняння такого виду: y2 = x3 + ax + b. Для a = 0 і b = 7 (версія, що використовується біткоїном), воно має такий вигляд:

Еліптичні криві мають корисні властивості. Наприклад, невертикальна лінія, що перетинає криву у двох точках, завжди перетинатиме третю точку на кривій. Інша властивість — невертикальна лінія, дотична до кривої в одній точці, точно перетне іншу точку на кривій. Можна використовувати ці властивості для визначення двох операцій: додавання точки і подвоєння точки.

Для додавання точок, P + Q = R, через точки P і Q проводиться пряма, яка перетинає криву в третій точці R.

Потім знаходиться точка на кривій, симетрична третій точці R відносно осі x. Точка R і буде вважатися сумою P і Q. Приклад:

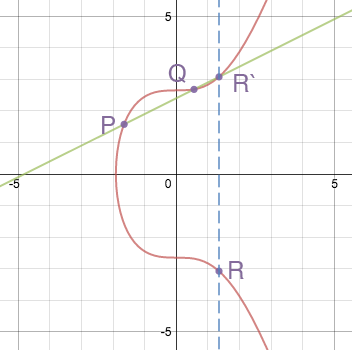
Аналогічним чином, під час подвоєння точки проводиться пряма, дотична до еліптичної кривої в точці P, яка має перетинати її ще в одній точці R.

Точка R, симетрична R’ відносно осі x, і буде вважатися точкою подвоєння P. Приклад:

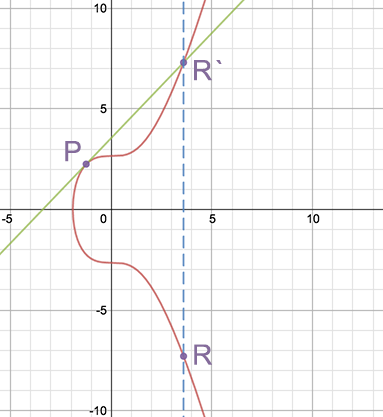
Разом дві ці операції використовуються для операції добутку на скаляр, R = a P, що визначається як додавання точки P до себе a раз. Наприклад:

R = 7P R = P + (P + (P + (P + (P + (P + (P + (P + (P + P)))))

Процес добутку на скаляр зазвичай спрощується за допомогою комбінації операцій додавання і подвоєння точок.

R = 7P R = P + 6P R = P + 2 (3P) R = P + 2 (P + 2P)

Тут 7P розділяється на два кроки з подвоєння точки і два кроки з додавання точки.

Що таке кінцеві поля?

Кінцеве поле в контексті ECDSA можна розглядати як заданий діапазон позитивних чисел, у який має потрапляти кожен розрахунок. Будь-яке число за межами цього діапазону обертається таким чином, щоб воно потрапляло в діапазон. Якщо результат операції виходить за межі цього діапазону, то після закінчення діапазону відбувається повернення до його початку, і розрахунок триває.

Найпростіше — розглядати цей процес як розрахунок операції "залишок від цілочисельного ділення", або оператор modulus (mod). Наприклад, 9/7 дає 1 із залишком у 2:9 mod 7 = 2. Тут кінцеве поле — від 0 до 6, і всі операції за модулем 7, над яким би числом вони не здійснювалися, дають результат, що потрапляє в цей діапазон.

Як відбувається об’єднання кривих з кінцевими полями?

ECDSA використовує еліптичні криві в контексті кінцевого поля, що значно змінює їхній зовнішній вигляд, але не фундаментальні формули або особливі властивості. Те ж саме рівняння, наведене на графіку вище, у кінцевому полі за модулем 67 має такий вигляд:

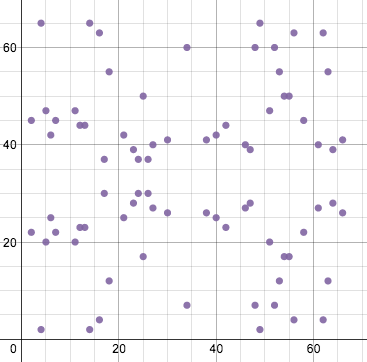
Тепер це набір точок, у якому всі значення x і y є цілими числами між 0 і 66. При цьому крива, як і раніше, зберігає свою горизонтальну симетрію.

Додавання і подвоєння точок тепер візуально трохи змінилося. Лінії, накреслені на цьому графіку, будуть обертатися навколо поля, зберігаючи той самий нахил. Тому додавання точок (2, 22) і (6, 25) виглядає так:

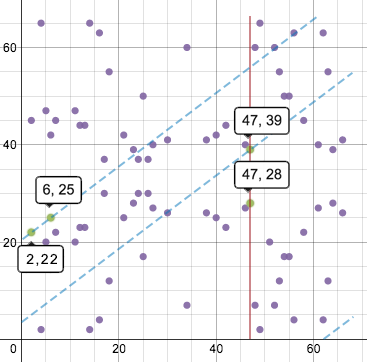
Пряма, що обертається і проходить через ці дві точки, у підсумку впирається в третю точку (47, 39), а симетрична їй відносно осі x буде (47, 28). Ця точка — результат операції.

Як ECDSA працює в біткоїні?

Такий протокол, як біткоїн, обирає набір параметрів для еліптичної кривої та репрезентацію його кінцевого поля, яка фіксована для всіх користувачів протоколу.

Параметри включають саме рівняння, просте значення модуля поля і базову точку на кривій. Порядок базової точки, яку не обирають незалежно, але яка є функцією інших параметрів, можна уявити графічно як число додавань точки до себе доти, доки її нахил не стає нескінченною (вертикальною) лінією. Базова точка вибирається так, що порядок — це велике просте число.

Для базової точки простого модуля і порядку біткоїн використовує дуже великі числа. Надійність алгоритму залежить від того, що ці величини величезні — це робить непрактичним використання брутфосу або інженерного аналізу.

У випадку біткоїна:

Рівняння еліптичної кривої: y2 = x3 + 7

Простий модуль = 2^256 — 2^32 — 2^9 — 2^8 — 2^7 — 2^6 — 2^4 — 1 = FFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFE FFFFFC2F

Базова точка = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Порядок = FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

Ця реалізація відома як secp256k1 і є частиною сімейства рішень еліптичної кривої в області скінченних полів, запропонованих до використання в криптографії.

Які недоліки ECDSA?

У ECDSA як поточному методі підпису в біткоїні відсутня нативна підтримка мультипідписів, тому їх реалізують за допомогою стандартизованого смарт-контракту Pay-to-Script-Hash (P2SH), який передбачає включення до блокчейну лише хешів скриптів.

Це здавалося б випадкове число визначає право власності на монети. У момент витрати власник розкриває скрипт і ключ для розшифровки хеша одночасно. Потім кожен користувач може використовувати початковий хеш для перевірки істинності скрипта і виконання умов витрати. Однак при цьому користувачі повинні розкривати всі умови витрати, включно з тими, які не були виконані. Наприклад, монети можуть бути витрачені тоді і тільки тоді, коли Боб і Аліса підпишуть транзакцію, або Аліса підпише її особисто після закінчення тижня, або це зробить Боб, надавши при цьому секретне число.

Перша проблема такої моделі — брак приватності. Для P2SH-транзакцій необхідно, щоб адреси починалися з цифри 3. Це дає блокчейн-аналітикам можливість розпізнати всі P2SH-транзакції в мережі та визначити адреси, що беруть участь у мультипідписі.

Друга проблема — великий масив даних для обробки, оскільки P2SH вимагає знання відкритих ключів усіх учасників мультипідпису.

Ці проблеми вирішують схема підписів Шнорра і технологія Taproot.